单选题
x=1/n(n=2,3,…)是函数f(x)=x·[1/x]的([·]为取整函数)( )。
A无穷间断点
B跳跃间断点
C可去间断点
D连续点
正确答案
答案解析
因x→(1/n)-时,n+1>1/x>n,[1/x]=n;x→(1/n)+时,n-1<1/x<n,[1/x]=n-1;故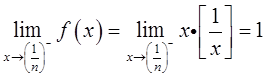
即x=1/n(n=2,3,…)是f(x)的跳跃间断点。
A无穷间断点
B跳跃间断点
C可去间断点
D连续点
因x→(1/n)-时,n+1>1/x>n,[1/x]=n;x→(1/n)+时,n-1<1/x<n,[1/x]=n-1;故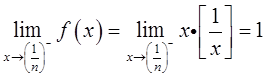
即x=1/n(n=2,3,…)是f(x)的跳跃间断点。